Disclaimer: I assume familiarity with machine learning and a general sense of how feed forward (i.e., the most basic type of) neural networks work for the contents of this article to be particularly valuable to the reader.

Predicting the next item in a sequence is the central theme of several natural language processing and time series prediction tasks. All the data concerned could be considered as sequences of numbers or characters (which are usually encoded as numbers in several ways). Whether forecasting weather, commodity prices or predicting the aggregate sentiment with respect to a consumer brand, this type of machine learning problem is widely seen in industry. Let’s look at how convolutions, normally associated with convolutional neural nets for computer vision, work with respect to sequence data.

The idea of convolutions is most often encountered in the context of Convolutional neural networks for computer vision related tasks e.g., convolutional neural nets for image classification, localization, and regression (yes regression, that’s not a typo. e.g., predicting weight of a dog/ fruit based on an image)

In a textbook use case, a 2D grid of parameters i.e., a filter, is slid across the pixels of the image, where at each stride, the pixels and the parameters are multiplied element-wise and summed. Once this is done to the entire image, the convolved output is pooled. This process is repeated for however many times the neural net architecture prescribes and then fed to a typical feedforward neural network. (TLDR: a stack of convolution/ pooling operations then a fully connected network). Usually, multiple filters are used and the best weights for each filter are learned using back propagation and gradient descent.

Long story short, the convolutions reduce the information in the image to result in features that provide an increase in predictive performance to the fully connected layer (hence the whole neural network). The alternative of directly feeding in pixel values to a fully connected network is sub-optimal and riddled with issues.

TLDR: 2D convolutions distill features from 2D pixel arrays which we call images

Now I want to illustrate how this process can be applied for series (or sequence) data.

Series data is 1D. So, the filter would be 1D as well. The element-wise multiplication would look like this

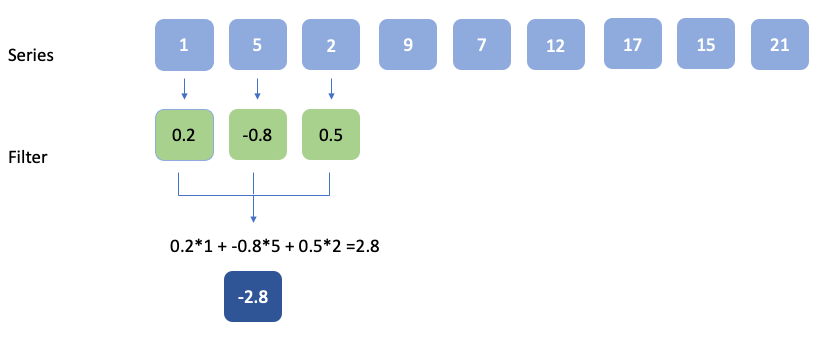
As in the case of 2D convolutions, the filter is moved by a certain step i.e., a stride. When the stride is 1 and the entire convolution operation looks like this

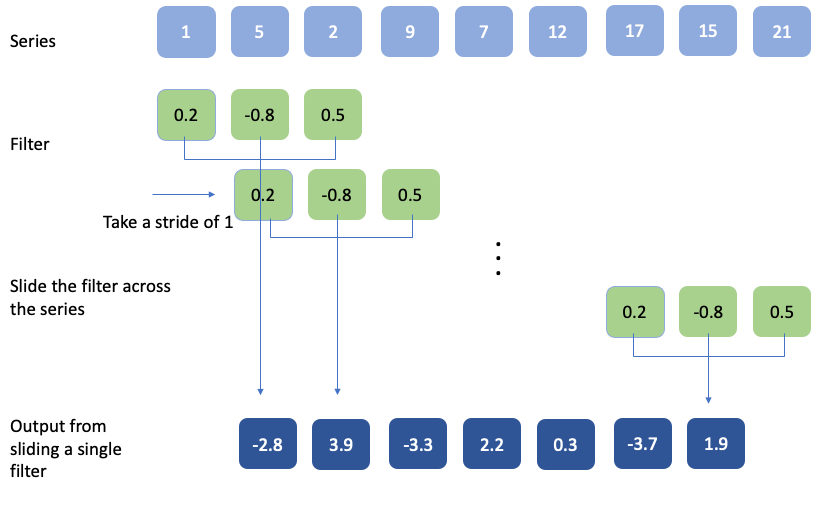
Usually, multiple filters are applied and the output, i.e., the distilled series features, are fed into a fully connected layer for the actual prediction. The actual weights of the filters, which are randomly initialized, are learned during the training of the neural net.

You could think of 1D and 2D convolutions as feature engineering sub-units of a neural network architecture.

A code snippet for a neural network leveraging 1D Convolutions implemented using TensorFlow looks like follows.

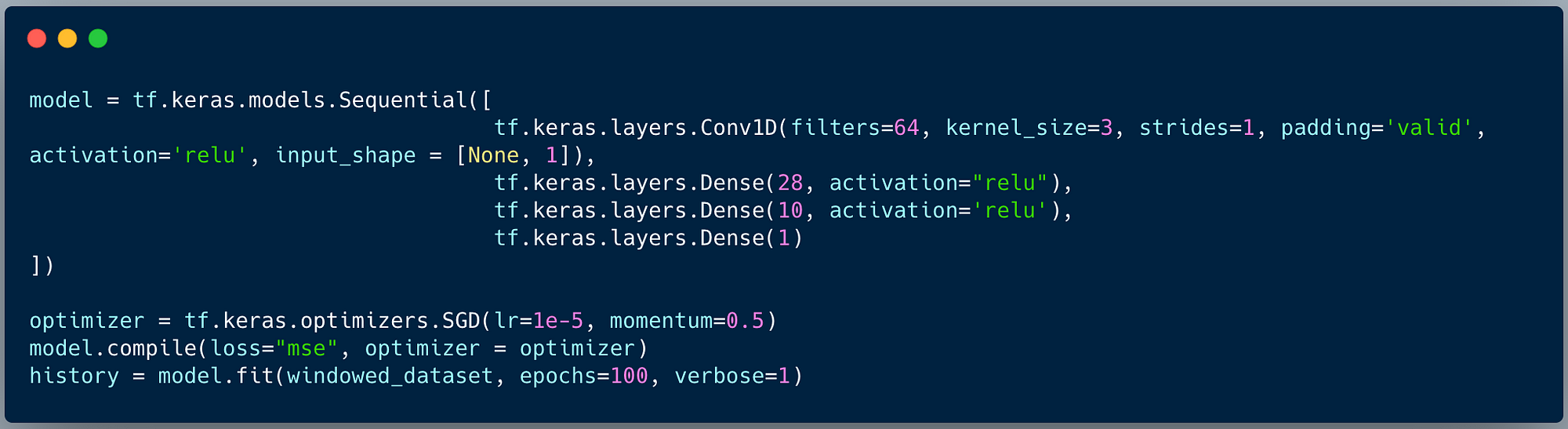
There are 64 filters, each of 3 elements in length (kernel_size). The padding we use in this case is ‘valid’ (i.e., no padding) and the stride is 1 (just like in the example). The specific example is from a time series use case where a windowed dataset is created for time series prediction, but the same general architecture could be mapped to a natural language processing use case.

In practice, I would recommend trying this approach and using a hyperparameter optimization framework like Keras Tuner, Hyperopt or Optuna to experiment with the number of convolution layers, kernel sizes and stride lengths.